- · 《数学杂志》期刊栏目设[01/26]
- · 《数学杂志》投稿方式[01/26]
- · 数学杂志版面费是多少[01/26]
数学的奇思妙想2:正多面体知多少?强基的天才
作者:网站采编关键词:
摘要:线性代数(高等代数)教学日记:对偶空间续 对偶空间即使对我这个端数学饭碗的来说,也是妙到极致的体验,想到柏拉图学派两千多年前就利用这个思想和方法确定了所有正多面体,
线性代数(高等代数)教学日记:对偶空间续
对偶空间即使对我这个端数学饭碗的来说,也是妙到极致的体验,想到柏拉图学派两千多年前就利用这个思想和方法确定了所有正多面体,让人感慨万千。
我一直都不知道有多少种正多面体,中学时一直坚定地认为有无穷多种,和正多边形一样,然后上大学了,就被打了脸。中学好像也不教这些东西,因为高考不考,我们强基计划班的天才们绝大部分也不知道,可见高考数学大纲大有问题。
平常说的正多面体被称为柏拉图正多面体,是指凸正多面体,有且仅有五种:4,6,8,12,20。这让我一直耿耿于怀:太少了,空间这么大,规则的石头怎么就这么少?
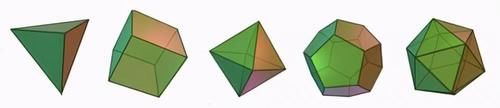
欧几里得在几何原本中有简洁漂亮的证明,只用到一个比较容易接受的事实:即空间角的面角之和必定小于2π(等于的话就变成平面了),因此正多面体的面只可能是正三边形(三种),正方形(一种)和正五边形(一种)。网上有些证明用到欧拉示性数公式,虽然高大上,但晚了两千年呢!
柏拉图正多面体和对偶空间有什么关系?
两个正多面体称为是对偶的如果一个是由另一个的面心作顶点得到的。比如正方体有6个面,以这6个面的中心为顶点作出的多面体恰好是正八面体。因此,正六面体与正八面体互为对偶;类似地,正十二面体与正二十面体互为对偶。问题来了,既然正多面体都是两两对偶,哪正多面体的总数应该是偶数啊?
呵呵,正四面体和自己对偶!这称为自对偶。
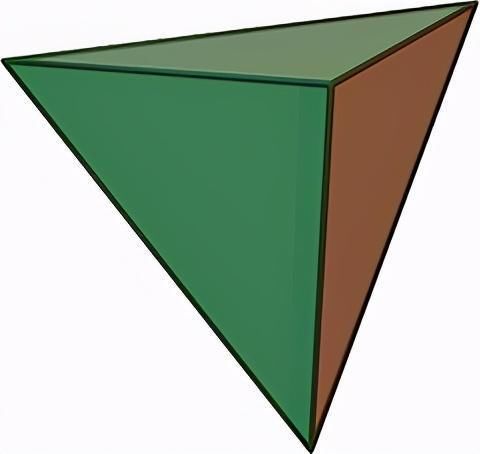
不看不知道,数学真奇妙!
好了,得请大家运动一下脑子了:高维有没有正多面体这种东东啊?如果有,变多了还是变少了?评论区里等你的回答哦!
文章来源:《数学杂志》 网址: http://www.sxzzzzs.cn/zonghexinwen/2021/0401/623.html