- · 《数学杂志》期刊栏目设[01/26]
- · 《数学杂志》投稿方式[01/26]
- · 数学杂志版面费是多少[01/26]
数学是所有科学的女王,如果你打算放弃数学,
作者:网站采编关键词:
摘要:对大多数人来说,数学以算术开始,以代数或微积分结束,但数学的范围比你想象的要大得多。 雪花的六重对称性是水分子对称性的直接结果,可以通过现代代数来研究。 对许多人来
对大多数人来说,数学以算术开始,以代数或微积分结束,但数学的范围比你想象的要大得多。

- 雪花的六重对称性是水分子对称性的直接结果,可以通过现代代数来研究。
对许多人来说,数学无非就是算术、几何、代数和微积分。即使是像工程这样的技术性较强的学科,也只会在列表中加入微分方程、偏微分方程、统计学,也许还有线性代数。而且,尽管这些数学子领域相当重要,但它们远远不是数学的所有。
数学课的主题
在开始之前,我想强调一条特别的线索,它几乎出现在所有的高等数学课上:证明。在非数学专业的数学和数学密集型课程中,你的大部分精力都花在学习:
- 如何为一个问题建立一个模型。
- 写出一些适合该模型的数学公式(通常是微分方程或线性方程组)。
- 然后按照一套特定的步骤来获得相关信息。
在更高层次的数学课上,你还必须证明一些东西,在这种情况下,你的大部分精力都花在学习:
- 如何为一个问题建立一个模型。
- 写出一些适合该模型的数学知识(通常是某种函数或算法)。
- 然后按照一系列特定的步骤来证明这个陈述。
你可能会注意到,这些步骤相当相似,这并不是巧合。虽然证明和计算密切相关,但人们往往更经常地与计算打交道,因此不熟悉证明中使用的技术。出于这个原因,许多大学要求数学学生上一门课,重点是如何写证明。大学将这门课称为高级数学入门。非数学专业的学生可能不会上这门课,我不会在本文中提到它,因为它本身不是目的,我想写一篇关于如何在数学中证明“东西”的文章,类似于我为基础物理学写的那篇文章。
迈出成为物理学大师的第一步,应该这样去求解物理学问题
下面是一个数学学生在微积分、微分方程和偏微分方程之外可能选修的不同科目的清单,这些科目包括什么,以及每个科目的实际用途。要明确的是,这并不意味着数学需要有直接的实际用途才值得学习。数学本身就很美,而数学发明可能需要几个世纪的时间才能变得不仅实用,而且必不可少,数论是现代密码学的基础,就是一个典型的例子。
离散数学
让我们从离散数学开始。微积分处理的是平滑、连续的函数,而离散数学则是一个广泛的领域,涉及任何可以被分离成离散对象的东西。所有计算机科学系学生和电气工程师都必须上这门课。在标准的课程中,会涉及形式逻辑、计数问题和图论(不是像f(x)=x^2这样的图,而是更像城市和道路的图,它们都是有向无环图)等主题。这门课往往是学生们必须证明的第一门课(也是最后一门)。

我们什么时候会用到离散数学?
正如我已经说过的,离散数学是电气工程和计算机科学的必修课。在电气工程中,控制一个电路的每个部分获得多少电流需要使用图论,而实现数字逻辑需要使用形式逻辑。计算机科学中的大量问题涉及到识别何时可以用图来模拟一个系统,然后使用图论中的一些东西来简化问题。例如,谷歌的网页排名算法将网页建模为节点,将链接建模为有向边,然后它可以使用图论来研究。
计数问题可能看起来没什么用,但它们在概率论和统计学中出现得很多。在统计力学中,熵将允许你把寻找一个系统的各种物理属性(如体积、能量、成分、热容量等)之间的关系的问题转换成一个计数问题,正如你可以在文章从零推导出理想气体定律,一项浩大的工程,涉及数理化三个领域中看到的那样。使用统计力学将热力学问题变成计数问题的最典型的例子必须是爱因斯坦模型。
爱因斯坦模型是晶体固体的模型,它包含了大量的相同频率的独立三维量子谐振子。在德拜模型中,独立性假设是松弛的。
实分析
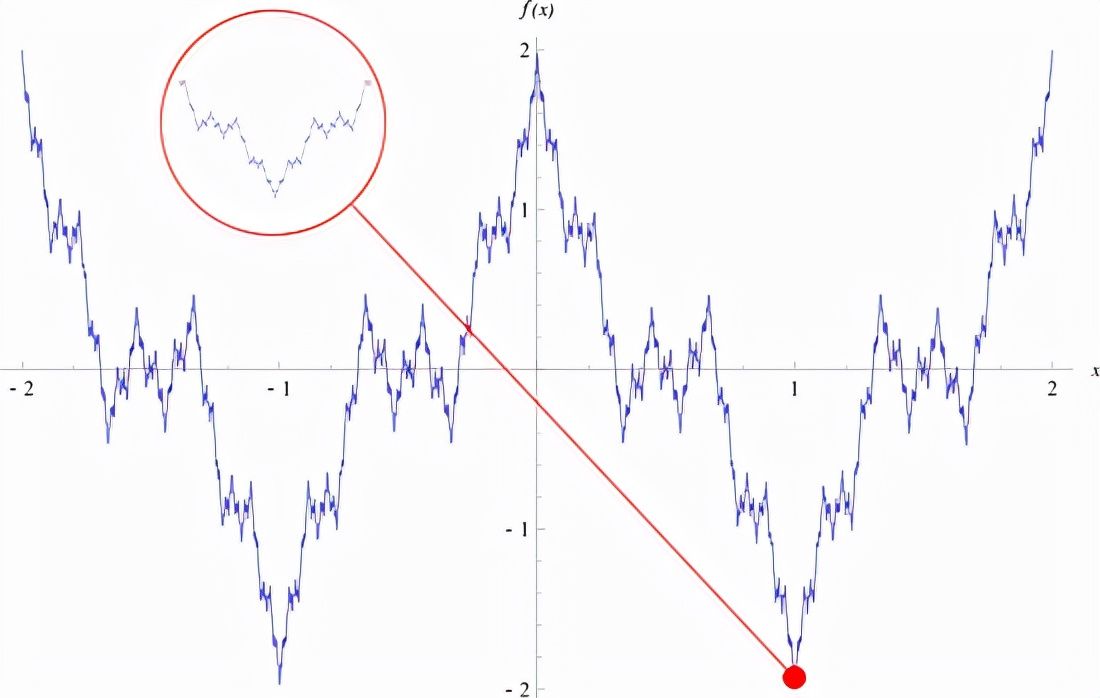
我们已经介绍了离散数学,让我们来看看微积分的核心——
文章来源:《数学杂志》 网址: http://www.sxzzzzs.cn/zonghexinwen/2021/1031/1518.html