张益唐被曝已证明黎曼猜想相关问题，震动数学

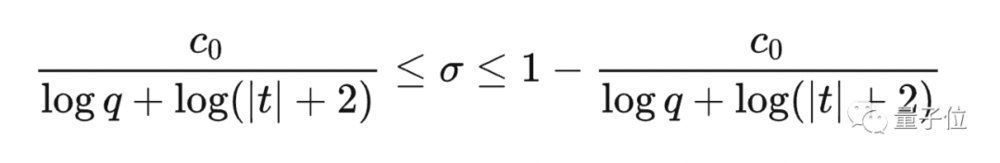
而为了研究等差数列上的素数分布，数学家Dirichlet引入了L函数。

很明显，这个公式的限制条件要多了许多，所以大家当然希望L函数能够没有异常零点。

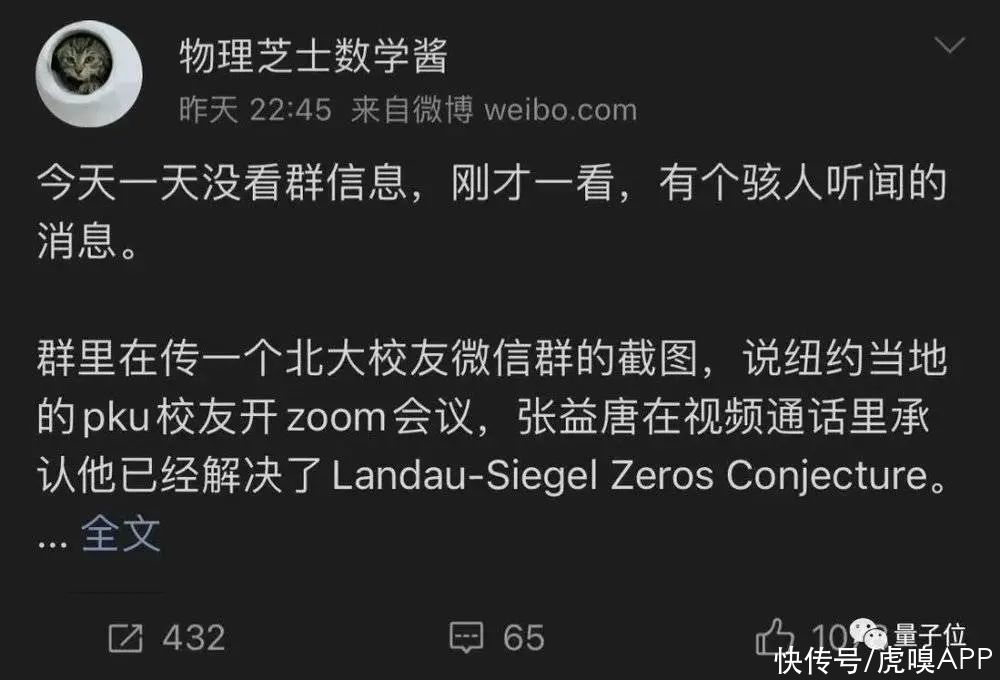
而这则消息，据说是张益唐在参加北京大学校友Zoom线上会议时亲口所述。

而在这篇论文发表之前，他曾有令人羡慕的中外顶尖学府求学经历，但随后却经历了多年的蛰伏，甚至不得已跑去赛百味端盘子。

1999年，张益唐与唐朴祁合作发表一项互联网专利。这项专利涉及一个实用性很广的计算机算法难题，但张益唐只用了3周的时间就搞定了，这令唐朴祁对其刮目相看。

再后来，数学家也发展出了对应的解析工具来说明L函数在σ=1时无零点，从而证明了等差数列上的素数定理：

参考链接：

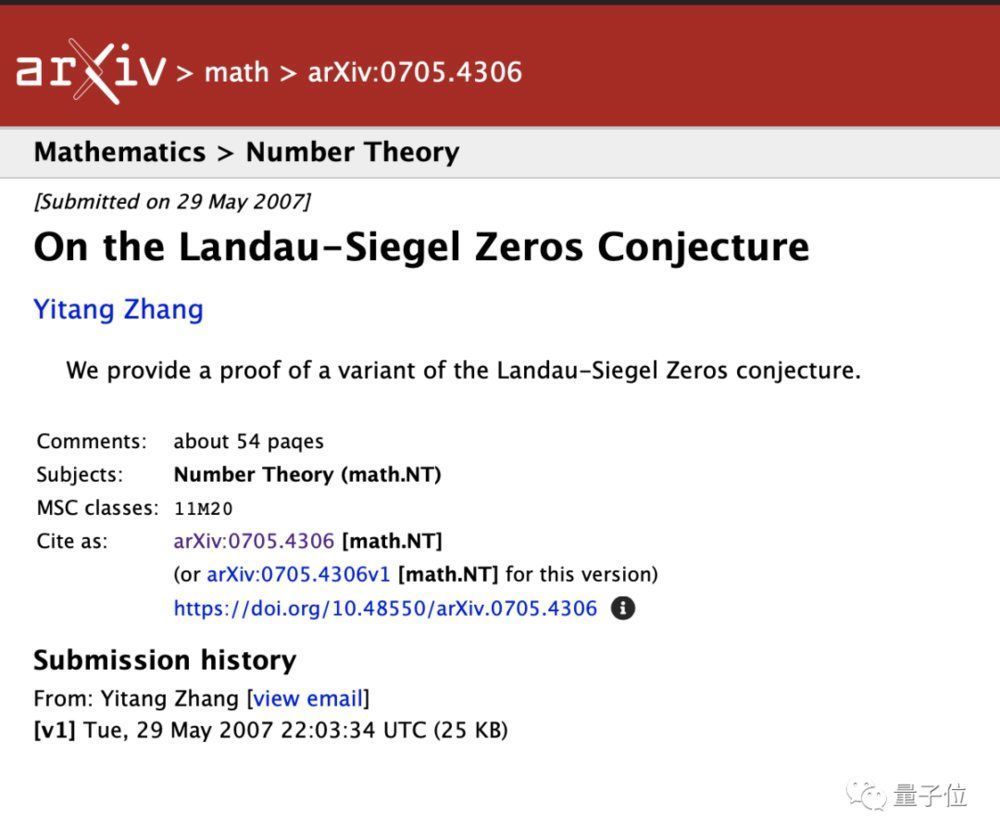
实际上，关于朗道-西格尔猜想，早在2007年老张就曾预印了一篇论文，但是里面的论证有些Bug。

对它的证明，又为何会引发如此反响？

首先我们设实数σ，t和复数s=σ+it。

所以他希望博士毕业以后离开这个圈子，回头去研究他感兴趣的数论，但导师莫宗坚得知后并不高兴，于是两人分歧越来越大。

1978至1985年，张益唐在北大数院拿到了本科和硕士学位，并在硕士期间师从我国著名数学家潘承彪。

如此爆料，可谓是在数学界轰动不已。

考虑张的平生，其人沉稳坚毅，肯定不会信口胡说。

半生蛰伏，一鸣惊人

并且根据这条爆料消息来看，相关文章将会在11月初发到预印本网站，一百多页。

后来Walfisz利用这个更弱的非零区域得到了一个妥协版的等差数列素数定理：

所谓朗道-西格尔零点猜想，简单来说就是黎曼猜想的某种弱形式。

此后，他多次提到过他正在关注这个问题。

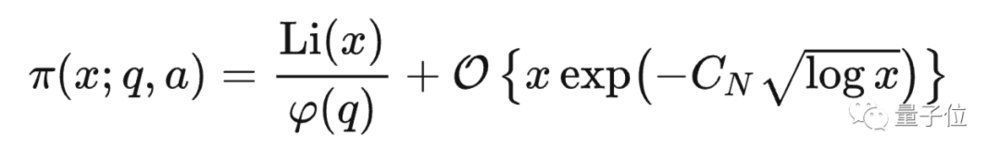
但幸运的是，Landau证明了对于每个这样的L函数，若下面区域中存在异常零点，则这样的零点只可能出现一个，而且阶数也恰好只能是一。

然后在2019年，张曾表示在这个猜想上已取得一些可喜的进展。

如果L函数所有的非平凡零点都落在这个区域内，就可以得到带余项的等差数列素数定理。

后来代数几何学家莫宗坚访问北大，并发掘了张益唐。随后张益唐就跟着莫宗坚飞往美国，到普渡大学（号称“太空人的摇篮”那个）读博。

至于具体证明了什么，还需要等待张益唐本人的正面回复了。

想涨知识 关注虎嗅视频号！

[2]https://www.zhihu.com/question/559674941

本文来自微信公众号：量子位 （ID：QbitAI），作者：金磊、Alex，头图来自：视觉中国

网传数学家张益唐，已经攻克了朗道-西格尔零点猜想（Landau-Siegel Zeros Conjecture）。

[5]https://weibo.com/2703634217/MatuJ2kAe?type=comment

于是，唐朴祁向在新罕布什尔大学任教的学弟葛力明介绍张益唐，然后经葛力明推荐，张益唐先后在这里担任数学系与统计学系的助教和讲师，执教微积分、代数、初等数论等课程。

曾有朋友向张益唐建议转行从事金融或计算机行业，但他并不愿意。

一边是继续苦苦钻研数论；另一边，他也不得不四处谋生，但可惜在很长时间内，他都没找到好工作，有时甚至只能借住朋友家的地下室。

End

因此，要是张益唐证明的是朗道-西格尔零点，那么黎曼猜想是错的。

于是前人证明了L函数的非平凡零点基本上都能落在类似于下面公式中的沙漏型的区域：

那一年，他在数学最高期刊Annals of Mathematics上发表了震惊众多学者的《质数间的有界间隔》。

这也就是为何大家都对这则消息都用“骇人听闻”来形容了。

微博博主“物理芝士数学酱”认为，如果张益唐所证明的是朗道-西格尔零点存在，那么黎曼猜想就可以死了：

而断言L函数没有异常零点的猜测就被称为Landau-Siegel猜想。

再加上他性格偏内向，以及在读博期间发表的学术论文太少等因素，竟没有任何一个美国大学或研究所愿意要他。

核心要回答的一个问题就是：是否存在一个叫做朗道-西格尔零点的东西。

本内容为作者独立观点，不代表虎嗅立场。未经允许不得转载，授权事宜请联?p>

文章来源：《数学杂志》 网址: http://www.sxzzzzs.cn/zonghexinwen/2022/1017/1974.html